מחשבון חישוב היקף מעקל
עוד מימי יוון העתיקה התעניין האדם בגאומטריה ובצפונות המספרים העומדים מאחורי המתמטיקה של הטבע. אחת החידות הפשוטות מחד, אך מורכבות מאידך, היא חישוב היקפו של המעגל. חישוב היקף המעגל הלך והשתכלל במהלך ההיסטוריה, עד למציאת הקבוע פאי, אשר דייק את החישוב, וקירב אותו לשלמות.
קודם כל – מה זה מעגל?
מעגל הינו אוסף הנקודות הרחוקות מרחק מסוים מנקודה מוגדרת. המרחק קרוי "רדיוס המעגל", והוא מסומן על פי רוב באות R. קוטר המעגל מוגדר להיות פעמיים הרדיוס שלו, כלומר הקו החוצה את המעגל מקצה לקצה.
מה זה היקף של מעגל?
היקף המעגל, כשמו כן הוא, מתייחס לגודל ההקפה של הצורה במרחב הדו ממדי. ניתן לומר שהיקף המעגל הינו הקו התוחם את שטח המעגל, ועל מנת למצוא את גודלו (ללא מדידה פיזית), יש למצוא נוסחה שתקשר בין היקף המעגל לרדיוסו. היחס בין הרדיוס להיקף מתבקש, היות וככל שהרדיוס גדול יותר כך היקף המעגל גדול יותר.
איך מחשבים היקף מעגל
נתחיל מהסוף – חישוב היקף מעגל בהינתן קוטרו נעשה בצורה הבאה:
2πR = היקף המעגל
כאשר R מסמל את הרדיוס, כזכור.

אם נרצה להתנסח במילים – היקפו של מעגל שווה לפעמיים הרדיוס שלו (קוטרו), כפול הקבוע פאי. ניתן לומר בצורה ויזואלית שהקבוע פאי הוא מספר המייצג את היחס בין קו ישר לקו מעגלי, ולכן היקף המעגל שווה לפעמיים הקו הישר החוצה את המעגל. מתוך משוואה זו ניתן לבנות מחשבון היקף מעגל בצורה פשוטה – כל מה שיש לעשות הוא להזין את רדיוס המעגל והמחשבון יכפיל את הרדיוס בשתיים ויכפול בקבוע פאי לקבלת היקף המעגל. שימו לב כי לשם חישוב היקף מעגל על ידי קוטר יש לכפול את הקוטר בפאי, ללא הכפלה נוספת.
באופן הופכי ניתן ליצור מחשבון למציאת רדיוס המעגל בהינתן היקפו: המחשבון יחלק את ההיקף בערך ה-π, ויחלק ב-2. סדר פעולות זה הינו הסדר ההפוך מהמחשבון להיקף המעגל, ועל כן נקבל את התוצאה ההפוכה בדיוק.
ההיסטוריה של חישוב היקף המעגל
ייחודיותו של המעגל הינו בכך שהוא מעין מצולע בעל אינסוף צלעות. ניתן להמחיש זאת באמצעות השוואה בין ריבוע, מחומש, משושה, ומתומן. כפי שניתן לראות – ככל שמספר הצלעות גדול יותר כך הצורה הולכת ונעשית דומה יותר למעגל. עובדה זו מסייעת בהבנה שניתן לחשב את היקפו של המעגל אם נשווה אותו להיקף של צורות בעלות יותר ויותר צלעות.
חישובו של ארכימדס לקבוע פאי
ארכימדס פיתח תפיסה זו כאשר ניגש לבעיה באופן הבא:
היקף המעגל גדול יותר מהצורה הכלואה בתוכו, וקטן יותר מהצורה בה הוא כלוא. ניתן להמחיש זאת באמצעות סדרת הצורות הבאות:
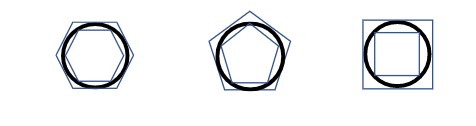
כפי שניתן לראות ככל שמספר הצלעות עולה, כך הדיוק של חישוב היקף המעגל הולך ומשתפר. המשך פעולה זו הביא את ארכימדס לזהות את ערכו של הפאי בין המספרים 3.140845 ל-3.142857.
קצת על הפאי
הפאי המדויק הינו מספר אינסופי, וספרותיו ההתחלתיות הן: ……3.1415926535. על פי רוב, נהוג להתייחס לפאי כ-3.14, ואף יום הפאי הבינלאומי נקבע ל-14 במרץ מסיבה זו. הפאי משמש במגוון שימושים מתמטיים ופיזיקליים, כגון חישובי הסתברויות, תורת המשחקים, חישובים קוונטיים, חישובים הקשורים לתנועה הרמונית או תנועה מעגלית פיזיקלית ועוד. בשנת 2015 שינן רג'וויר מינה לא פחות מ-70,000 ספרות של ערך הפאי ללא טעות.
על ההבדל בין מעגל לעיגול
בשפה העברית נקבעו מספר מושגים המבחינים בין צורות גאומטריות שונות. המילה מעגל מתייחסת להיקף הצורה בלבד, ואילו המילה עיגול מתייחסת להיקף ולשטח הפנימי יחד. בגזרת המרובעים ההבחנה שונה – מרובע הינו השם אשר ניתן למשפחה הגאומטרית המכילה ארבע צלעות, הכוללת בתוכה את הריבוע, המלבן, הטרפז, הדלתון וכדו', כאשר לכל פרט מתקיימות תכונות ייחודיות המבדילות אותו מיתר המרובעים.
חישוב היקף של אליפסה
כאמור לעיל, עיגול הינו הצורה המתקבלת מחיבור כלל הנקודות הרחוקות במידה קבועה ממרכז המעגל. אליפסה הינה הצורה המתקבלת בצורה הבאה:
- נקבע שתי נקודות, ונקרא להן מוקדי האליפסה.
- נחליט על מרחק מסוים, ונקרא לו קבוע המרחק.
- נחבר את כלל הנקודות אשר סכום מרחקיהן משני המוקדים שווה לקבוע המרחק.
שימו לב כי אליפסה אשר שני המוקדים שלה מתלכדים יחד תיצור עיגול.
חישוב היקף האליפסה מורכב יותר מחישוב ההיקף של המעגל, ומקובל להשתמש בקירוב הבא:
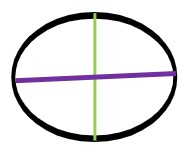
היקף אליפסה = חיבור הרדיוס הארוך והרדיוס הקצר ולכפול בפאי. או באותיות: P = π(R1+R2). (הרדיוס הקצר הינו חצי מהקוטר הקטן יותר של האליפסה (הקו הירוק), והרדיוס הארוך הינו חצי מהקוטר הרחב יותר של האליפסה (הקו הסגול)).
איך מחשבים היקף של ריבוע
היקף של ריבוע ניתן לחישוב בהינתן אחת הצלעות, ונוסחתו: 4h, כלומר ארבע פעמים הצלע. נוסחה זו מתבססת על כך שכל צלעותיו של הריבוע שוות. במקרה של מלבן בו רק שתי הזוגות של הצלעות המקבילות שוות, יש לכפול את הצלע הארוכה בשתיים ואת הצלע הקצרה בשתיים, ולחבר את שני המספרים יחד.
היקף של צורה תלת ממדית
קשה להתייחס להיקף של צורה כאשר מתייחסים לצורות תלת ממדיות. עם זאת, מקובל להתייחס לשטח הצורה כאל ההיקף שלה, מכיוון שהיקף הצורה מתאר את שטח הפנים החיצוני שלה בדומה להיקף בצורה דו ממדית. להלן נציג את הדרכים לחישוב ההיקף של מספר צורות תלת ממדיות נפוצות.
איך מחשבים היקף של קובייה תלת ממדית
על מנת לחשב את ההיקף של קובייה תלת ממדית, יש לחשב את שטח אחת הפאות ולהכפיל בשש (לכל קובייה יש שש פאות). שטחה של הפאה שווה לצלע כפול עצמה, או צלע בריבוע. אם כן, ניתן לבנות נוסחה לחישוב השטח של קובייה תלת ממדית:
h2*6 = שטח הקובייה התלת ממדית.
איך מחשבים היקף של גליל תלת ממדי
על מנת לחשב את היקפו של הגליל, עלינו לחלק אותו לשני חלקים: שטח הבסיסים ושטח המעטפת. את שטח הבסיסים ניתן לגלות באמצעות הנוסחה לחישוב שטח מעגל:
πR2 = שטח המעגל.
את השטח יש לכפול בשתיים, מכיוון שלגליל יש שני בסיסים (אחד למעלה ואחד למטה). על מנת לחשב את שטח המעטפת עלינו לחשב את היקף המעגל ולהכפיל בגובהו של הגליל, כך שהנוסחה המתקבלת הינה:
π2R*h = שטח המעטפת.
חיבור שתי הנוסחאות ייתן לנו את הנוסחה לחישוב היקף הגליל, בהינתן גובהו ורדיוסו.
איך מחשבים היקף של עיגול תלת ממדי
היקפו של כדור תלת ממדי הינו מורכב לתפיסה מבחינה אינטואיטיבית, אולם נוסחתו היא:
4πR2 = היקף מעגל תלת מימדי.
ניתן לראות שהיקפו של מעגל תלת ממדי שווה לפי 4 משטח המעגל בעל אותו הרדיוס. כדור תלת ממדי הינו הצורה בעלת שטח הפנים הקטן ביותר ביחס לנפח, ועובדה זו עשויה להסביר תופעות רבות המתרחשות בטבע, למה כמו בועות אוויר הן עגולות בנוזל, למה טיפת מים מתכדרת לכדור על מצע שומני, למה פירות או זרעים נוטים לקבל צורה עגולה, ועוד.
סיכום
הצגנו במאמר זה את הדרך הפשוטה לחישוב היקף מעגל, והרחבנו מעט בחישוב היקפים של צורות נוספות – דו ממדיות ותלת ממדיות. באתר שלנו ניתן למצוא מחשבון לחישוב היקף מעגל, לקבלת תוצאה מדויקת בצורה מהירה ופשוטה.
